Rozwiąż zagadki Kakuro

W tym przewodniku oferujemy szereg praktycznych wskazówek, jak rozwiązywać zagadki Kakuro, z trudnościami od poziomu początkującego do eksperckiego.

Podsumowując zasady: Kakuro to gra logiczna na planszy podobnej do krzyżówek, w której używane są cyfry, aby podsumować je do wartości określonych w kwadratach definicji planszy. Ponadto w każdej grupie sumy każda cyfra może pojawić się najwyżej raz.

Tradycyjny sposób rozwiązania zagadki Kakuro jest przyrostowy: korzystając z istniejących informacji na tablicy, możesz z pewnością znaleźć wartość określonej komórki, która może przyjąć tylko jedną możliwą wartość. Następnie ta wartość jest wypełniana i proces powtarza się, aż wszystkie komórki płyty zostaną odkryte.

W niektórych sytuacjach, nie ma konkretnej komórki płyty mającej tylko jedną możliwość. W takich przypadkach każda z możliwości musi zostać zbadana samodzielnie i wyeliminowana poprzez sprzeczności, dopóki nie pozostanie tylko jeden sposób działania.

Przedstawiliśmy poniżej kilka metod, aby zrobić postępy w rozwiązywaniu rzeczywistej zagadki.

Unikalne kwoty dla określonych definicji

Istnieje kilka definicji, które można rozwiązać tylko w określony sposób:

• suma 3 (w dwóch komórkach) zawsze będzie wynosić 1 + 2.
• suma 4 (w dwóch komórkach) zawsze będzie wynosić 1 + 3.
• suma 17 (w dwóch komórkach) zawsze będzie wynosić 8+9.
• suma 6 (w trzech komórkach) zawsze będzie wynosić 1 + 2 + 3.
• suma 24 (w trzech komórkach) zawsze będzie wynosić 7 + 8 + 9.

i tak dalej... Zwykle możesz najechać kursorem na siatkę Kakuro nad numerem definicji i pojawi się etykietka zawierająca wszystkie możliwości zapisu tej sumy z unikalnymi cyframi w liczbie dostępnych komórek.

Sumy, które można zapisać w unikalny sposób, to zazwyczaj niskie sumy lub wysokie sumy, które wymuszają niskie/wysokie cyfry w odpowiedzi, aby je osiągnąć.

Posiadanie unikalnego sposobu zapisywania sumy pomaga, ale pamiętaj, że wszystkie permutacje są ważne i nadal musisz dowiedzieć się, której rzeczywistej permutacji użyć na planszy.

Ograniczenia wiersza/kolumny

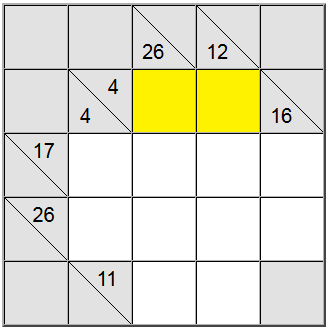
W przypadku zaznaczonych powyżej żółtych komórek istnieje tylko jeden sposób zapisywania sumy: 4 = 1 + 3. Jednak nadal musimy dowiedzieć się, której permutacji (1 + 3 lub 3 + 1) użyć.

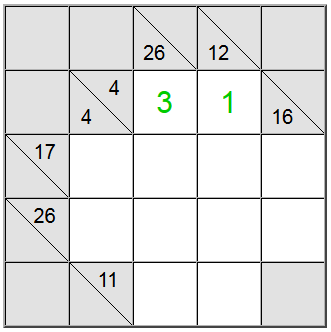
Okazuje się, że pomaga nam definicja pionowa 26: suma w 4 komórkach, która zawierałaby cyfrę 1, wynosiłaby co najwyżej 1 + 9 + 8 + 7 = 25. Ponieważ nasza suma wynosi 26, okazuje się, że cyfra 1 nie może być częścią sumy. Dlatego jedyne pozostałe zamówienie na żółte kwadraty to 3+ 1.

Definicje przecięcia

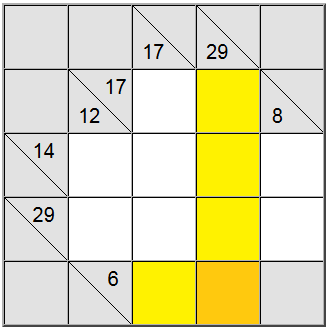
Na powyższej planszy poziome żółte kwadraty można zapisać jako 6 = 1 + 5 lub 6 = 2 + 4. Pionową żółtą sumę można zapisać tylko jako 29 = 5 + 7 + 8 + 9.

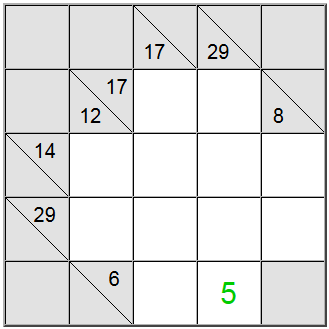
Żółty kwadrat znajdujące się na przecięciu tych dwóch definicji sumy musi zawierać tę samą cyfrę, więc w definicjach poziomych i pionowych musi być obecna wspólna cyfra, aby można ją było dzielić. Patrząc na powyższe możliwości, możemy łatwo zorientować się, że 5 jest jedyną cyfrą, która spełnia to kryterium.

Ta technika działa szczególnie dobrze, gdy przecinają niską sumę z definicją wysokiej sumy. Definicje o niskiej i dużej sumie to te, które mają względnie niską lub wysoką liczbę definicji sumy (odpowiednio 6 i 29 dla naszego przykładu) w porównaniu z liczbą dostępnych komórek. Ponieważ 6 jest stosunkowo niski, wymusi niskie cyfry w reprezentacji sumy, a 29 wymusi wysokie cyfry (w celu osiągnięcia tych sum przy użyciu podanej liczby komórek). Dlatego przecięcie niskich i wysokich cyfr prawdopodobnie będzie zawierało tylko jednego kandydata do rzeczywistej wartości komórki.

Min/max wartości dla grupy sumy

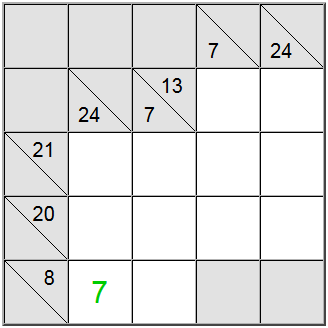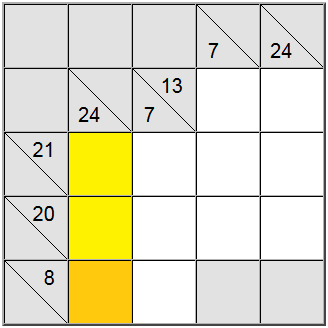
Czasami przydatne jest ustalenie maksymalnej lub minimalnej wartości dla grupy sumy. To może dać poczucie, jaki jest prawidłowy zakres cyfr dla tej konkretnej sumy, co z kolei pomoże Ci dokonać korelacji z innymi ograniczeniami i wymyślić unikalne zadania na tablicy.

W powyższym przykładzie żółte pionowe komórki akceptują tylko wartości równe 7 lub wyższej. Jeśli spróbujesz przypisać 6, możesz łatwo dowiedzieć się, że 6 + 9 + 8 = 23 więc suma definicji 24 nie byłaby osiągalna.

Ponieważ 7 jest minimum, definicja pozioma mająca 8 jako sumę wymusza 7 w tym położeniu.

Wniosek

Ćwiczenie to najlepszy sposób, aby zobaczyć, jak tę radę można zastosować w rzeczywistych grach Kakuro. Zagraj w puzzle na serio. Życzymy powodzenia i dobrej zabawy!

Odtwórz Kakuro